（x0,y0）=0,
(x0,y0)=02、奇点
设 P0(x0,y0)是曲线
F(x,y)=0
上的一点，假定函数F(x,y)在点P0有连续的偏导数，并且满足条件
（x0,y0）=0,(x0,y0)=0
则称P0是曲线F(x,y)=0的一个奇点.
如果函数F(x,y)在点P0(x0,y0)的二阶偏导数不全为零，那末称P0为曲线的一个二重点.设
则根据判别式
的符号在二重点中又可分出如下几种类型的奇点.
|
名称与图形 |
条件与性质 |
举 例 |
||||
|
结点
|
(i) (ii)曲线有两支通过点P0，且具有不同切线 |
双纽线
是以原点(0,0)为其结点
|
||||
|
孤立点
|
(i) (ii)在点P0的充分小的邻域里，除了点P0外，没有曲线上其他的点.
|
曲线
的轨迹是由直线x=1和原点(0,0)组成的，原点就是它的一个孤立点 |
|
|||
|
第一种尖点
|
(i) (ii)曲线由两支组成，在点P0有公共切线，这两支在其公共法线的同侧，而在公共切线的异侧.
|
半立方抛物线
是以原点(0,0)为其第一种尖点
|
|
|||
|
第二种尖点
|
(i) (ii)曲线由两支组成，在点P0有公共切线，这两支在其公共法线的同侧，又在公共切线的同侧. |
曲线
在原点的邻近有两支，即
它们在原点有公共切线，由于0<x<1,y总取正值，所以曲线在原点的邻近的两支都在公共切线和法线的同侧
|
|
|||
|
自切点
|
(i) (ii)曲线由两支组成，而彼此在点P0相切 |
曲线
由两条抛物线
组成，它们在原点彼此相切
|
|
|||
如果曲线由参数方程
x = x(t), y = y(t)
表示，那末当
=0，
=0时，由参数t0确定的点(x(t0),
y(t0))是曲线的奇点.
特别，曲线由极坐标方程
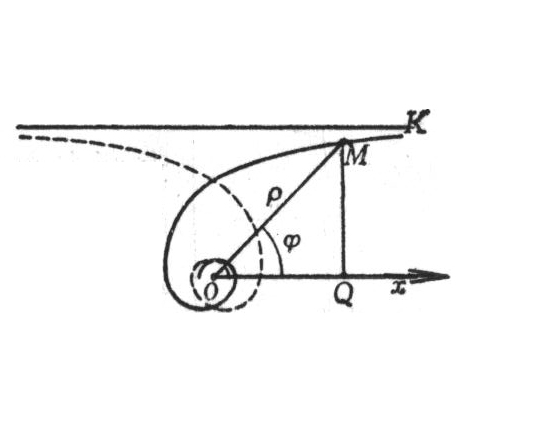
图 5.9
表示，那末当
=
=0时，点(
,
)是曲线的奇点.例如双曲螺线
当
∞时，
=0，所以极点是奇点.当极角
增大到无穷时，曲线上的点无限逼近于极点，但又不能达到（图5.9），所以这种奇点又称为渐近点.
<0
>0
